Hogyan tudunk elhelyezni egy fába vert szögön további szögeket?
Hozzávalók
- egy darab fa, benne egy viszonylag nagy szöggel
- szögek
magyarázat
Lásuk szögeink tömegközéppontját:
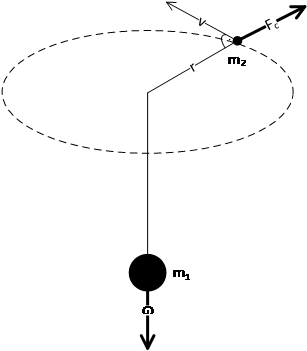
Vizsgáljunk először egy szögpárt, határozzuk meg a szögek tömegközéppontját, majd rajzoljuk meg a fellépő erőket. Ha szögnek nem lenne feje és hegye, akkor a tömegközéppont a szög felére esne, a fejnél lévő plusz tömeg illetve a hegyből hiányzó tömeg a középpontot egy kicsit a szög feje felé tolja. Az ábrán a két szög tömegközéppontjait M-el és S-el jelöltük, e pontokban fellépő nehézségi erőt G-vel és G1-el. (azonos szögek esetén G=G1) A nehézségi erőket felbontottuk a szögekkel párhuzamos illetve arra merőleges összetevőkre.
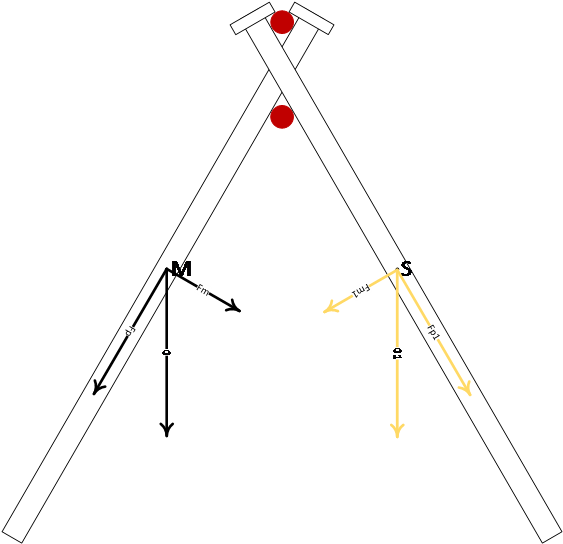
Alapvetően két kérdésre kell megtalálnunk a választ:
1. Miért nem csúsznak szét a szögek?
2. Miért nem borulnak le a szögek?
Miért nem csúsznak szét a szögek?
A szögek feje ugyan beleakad a keresztbe helyezett felső szögbe, de csak meglehetősen kis mértékben. Ha jobban megvizsgáljuk az ábrát, láthatjuk, hogy a szögek a nehézségi erőnek köszönhetően, emelőként működnek a keresztbe helyezett alsó szög, mint forgástengely körül. A két szög együtt úgy viselkedik, mint egy harapófogó, ez a „harapás” ami nem engedi a szögeket szétcsúszni. A fellépő forgató nyomatékokat az alábbi ábra szemlélteti:
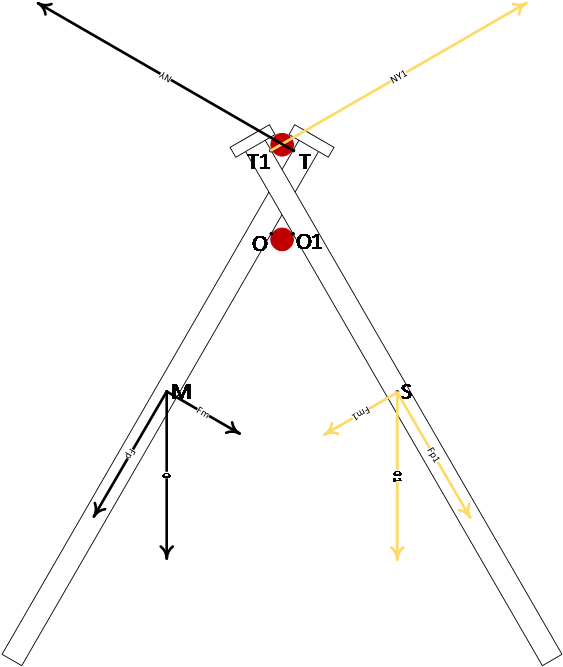
Az M pontban ható G erő merőleges összetevője (Fm) OM erőkaron „emeli” az O forgásponttól TO távolságra lévő felső kereszt szöget. A T pontban keletkező nyomatékot NY-el jelöltük. A nyomatékokat az alábbi összefüggés írja le:
Fm*OM=NY*TO
Mérésünk alapján TO=15 mm, OM=53 mm (M tömegközéppontot 2 mm-el toltuk a szög feje felé)
További mérési tapasztalatunk, hogy a két szög egymással 60 fokos szöget zár be, így G és Fm is 60 fokos szöget zár, amiből következik, hogy 2*Fm=G. (G és Fm egy egyenlő oldalú háromszög egyik fele) Mérési eredményeinket visszahelyettesítve a nyomatékokat leíró képletbe az alábbi összefüggést kapjuk:
NY=1,76*G
Tehát a T pontban fellépő NY „harapó”erő a szög teljes súlyának közel kétszerese.
A másik szögben is azonos erők hatnak, csak más irányokban, ezeket sárga színnel, illetve 1-es index-el jelöltük.
Miért nem borulnak le a szögek?
A válasz itt is a forgatónyomaték és a tömegközéppont körül keresendő. Keressük meg az összes felakasztott szög tömegközéppontját, mintha a szögek egy testet alkotnának.
Azt elfogadtuk, hogy egy homogén rúd tömegközéppontja a rúd felezőpontjára esik (aki nem hiszi, próbálja ki). Határozzuk meg egy szögpár tömegközéppontját, azzal a feltételezéssel élve, hogy a két szög teljesen egyforma. Az egyes szögek tömegközéppontjait már korábban meghatároztuk, így most egy 2 pontból álló pontrendszer tömegközéppontját kell megkeresnünk, ami azonos tömegek esetén a két pontot összekötő szakasz felezőpontja. Ábránkon K-val jelöltük, az itt fellépő nehézségi erő azonos a két szög súlyának összegével.
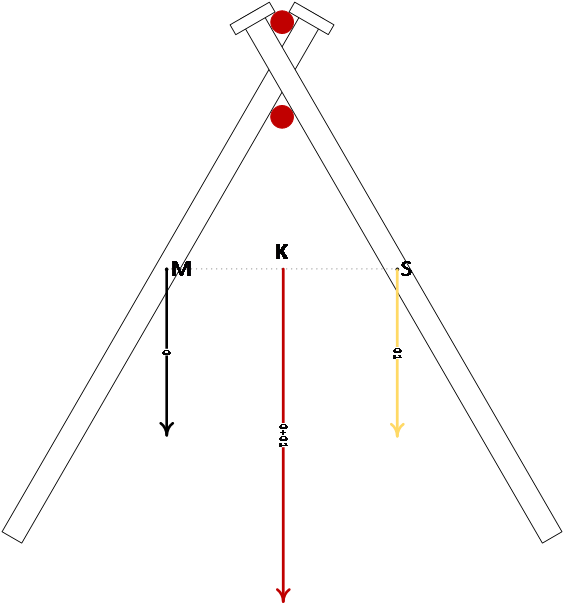
A bevezetőben nem említettük, de egy test tömegközéppontja eshet a testen kívülre is, mint például a mi esetünkben is.
Minden elhelyezett szögpárunk (ha egyforma szögeket használtunk) esetén a tömegközéppont a fentiekkel azonos lesz, tehát a szögpárjaink tömegközéppontjai egy egyenes szakasz mentén elhelyezkedő, azonos tömegű pontokból álló pontrendszert alkotnak. Ha a szögpárokat egyenletesen helyeztük el a keresztszögön, akkor a pontrendszer tömegközéppontja a szakasz felezőpontjára esik (K). Ha a keresztszöget úgy helyezzük el a tartószögön, hogy az alátámasztási pont (A) pontosan a K tömegközéppont felett helyezkedik el, akkor nem lép fel forgatónyomaték, mely leborítaná a szögeinket, hisz az erőkar 0. Kis mértékű pontatlanságot a rendszer magától „javít”, mert az esetlegesen fellépő forgató nyomaték a K tömegközéppontot közelíti az A pont függőleges tengelyéhez.
Oldalnézeti kép a teljes rendszerről.
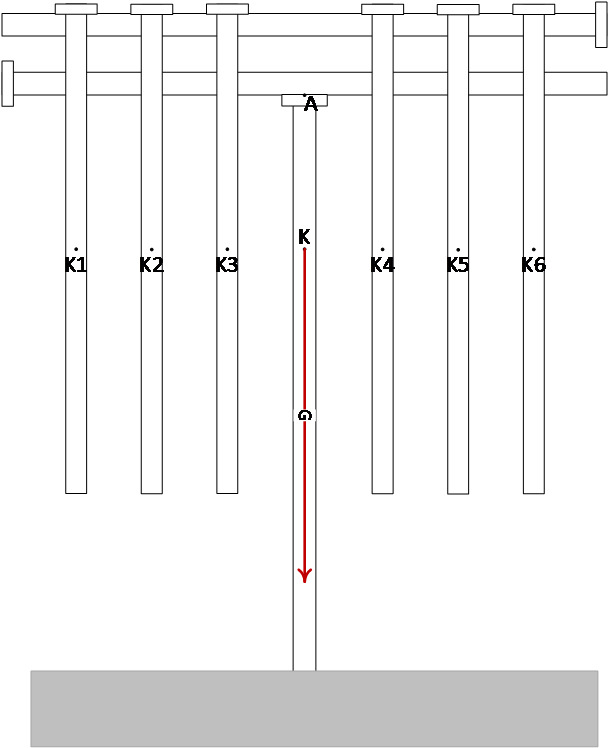
Így lehet elkészíteni